TensorFlow 시작하기(설치 이후 첫 튜토리얼)
이 블로그는 첫 번째 튜토리얼을 번역 후 필요에 따라 중간중간 설명을 첨가하였습니다.
원본 글은 https://www.tensorflow.org/ 에 포함되어 있습니다.
이 튜토리얼은 TensorFlow에서 프로그래밍을 시작하도록 안내합니다.
이 게시글을 읽기 전에 TensorFlow를 설치하십시오. 설치 방법은 이전 글에 있습니다.
이 가이드를 최대한 활용하려면 다음 사항을 알아야합니다.
파이썬으로 프로그래밍하는 법. (C#, Java는 해봤었습니다. 뭔가 유저 친화적이지만, 배우지 않았었기 때문에, 미흡한 점은 많습니다만, 구글링 및 튜토리얼 따라하면서 많이 배워가고 있습니다.
처음 하시는 분들도 두려워말고 도전하실 수 있습니다.)
최소한 배열에 대해서는.
이상적으로는 기계 학습에 관한 것입니다. 그러나 기계 학습에 대해 거의 또는 전혀 알지 못하는 경우에도 여전히 읽어야 할 첫 번째 가이드입니다.
TensorFlow는 여러 API를 제공합니다. 최저 수준의 API 인 TensorFlow Core는 완벽한 프로그래밍 제어 기능을 제공합니다. TensorFlow Core는 기계 학습 연구자 및 모델을 미세하게 제어해야하는 사람들에게 권장됩니다. 높은 수준의 API는 TensorFlow Core 위에 구축됩니다. 이러한 상위 수준의 API는 일반적으로 TensorFlow Core보다 배우고 사용하기가 쉽습니다. 또한 상위 수준의 API는 반복적 인 작업을 여러 사용자간에보다 쉽고 일관되게 만듭니다. tf.contrib.learn과 같은 고급 API를 사용하면 데이터 세트, 견적 도구, 교육 및 추론을 관리 할 수 있습니다. 메소드 이름에 contrib가 포함 된 상위 수준의 TensorFlow API 중 일부는 아직 개발 중입니다. 이후의 TensorFlow 릴리스에서 일부 contrib 메소드가 변경되거나 더 이상 사용되지 않을 수도 있습니다.
이 가이드는 TensorFlow Core에 대한 자습서로 시작됩니다. 나중에 tf.contrib.learn에서 동일한 모델을 구현하는 방법을 보여줍니다. TensorFlow를 아는 것보다 핵심적인 API를 사용할 때 핵심 원칙을 통해 내부적으로 일하는 방식에 대한 훌륭한 정신적 모델을 얻을 수 있습니다.
Tensor
TensorFlow에서 데이터의 중심 단위는 텐서입니다. 텐서는 임의의 수의 차원으로 배열 된 프리미티브 값 집합으로 구성됩니다. 텐서의 랭크는 차원 수입니다. 다음은 텐서 (tensors)의 몇 가지 예입니다.
3 # a rank 0 tensor; this is a scalar with shape []
[1. ,2., 3.] # a rank 1 tensor; this is a vector with shape [3]
[[1., 2., 3.], [4., 5., 6.]] # a rank 2 tensor; a matrix with shape [2, 3]
[[[1., 2., 3.]], [[7., 8., 9.]]] # a rank 3 tensor with shape [2, 1, 3]
+ 기존의 알고 있던 데이터 배열과는 살짝 다른 느낌입니다. 즉 집합의 개념으로 사용됩니다.
+ 텐서의 랭크는 차원의 수 라고 되어있는 것 처럼, 각 [ ] 괄호를 주의 깊게 보시면 대략적인 이해에 도움이 될 것입니다.
TensorFlow 핵심 자습서
TensorFlow 가져 오기
TensorFlow 프로그램에 대한 표준 import 문은 다음과 같습니다.
python
>>> import tensorflow as tf
+ 입력 후 ">>>"가 안보인다면, tensorflow 설치를 완료 안했을 경우가 많습니다.

이렇게하면 파이썬에서 TensorFlow의 모든 클래스, 메소드 및 심볼에 액세스 할 수 있습니다. 대부분의 문서에서는 이미이 작업을 수행했다고 가정합니다.
The Computational Graph
TensorFlow Core 프로그램은 두 개의 개별 섹션으로 구성되어 있다고 생각할 수 있습니다.
1.계산 그래프 작성. (Building the computational graph.)
2.전산 그래프를 실행합니다. (Running the computational graph.)
계산 그래프는 일련의 TensorFlow 작업을 노드 그래프로 배열 한 것입니다. 간단한 전산 그래프를 작성해 봅시다. 각 노드는 0 이상의 텐서를 입력으로 사용하고 텐서를 출력으로 생성합니다. 노드의 한 유형은 상수입니다. 모든 TensorFlow 상수와 마찬가지로 입력을받지 않으며 내부적으로 저장하는 값을 출력합니다. 다음과 같이 두 개의 부동 소수점 Tensors node1과 node2를 만들 수 있습니다.
node1 = tf.constant(3.0, tf.float32)
node2 = tf.constant(4.0) # also tf.float32 implicitly
print(node1, node2)

마지막 print 서술문은
Tensor("Const:0", shape=(), dtype=float32) Tensor("Const_1:0", shape=(), dtype=float32)
Tensor("Const:0", shape=(), dtype=float32) Tensor("Const_1:0", shape=(), dtype=float32)
Tensor("Const:0", shape=(), dtype=float32) Tensor("Const_1:0", shape=(), dtype=float32)
예상대로 노드 인쇄는 3.0과 4.0 값을 출력하지 않습니다. 대신 평가할 때 각각 3.0과 4.0을 생성하는 노드입니다. 노드를 실제로 평가하려면 세션 내에서 계산 그래프를 실행해야합니다. 세션은 TensorFlow 런타임의 컨트롤과 상태를 캡슐화합니다.
다음 코드는 Session 객체를 만든 다음 run 메소드를 호출하여 node1과 node2를 계산할 수있는 계산 그래프를 실행합니다. 다음과 같이 세션에서 전산 그래프를 실행합니다.
sess = tf.Session()
print(sess.run([node1, node2]))
3.0과 4.0의 예상 값을 봅니다.

Tensor 노드를 연산과 결합하여 더 복잡한 계산을 할 수 있습니다 (연산도 노드입니다). 예를 들어 두 개의 상수 노드를 추가하고 다음과 같이 새 그래프를 생성 할 수 있습니다.
node3 = tf.add(node1, node2)
print("node3: ", node3)
print("sess.run(node3): ",sess.run(node3))

+ 위의 결과되로 표시 되었다면 노드의 값을 tf.add를 통해 합쳐진 것을 볼 수 있습니다.
TensorFlow는 전산 그래프의 그림을 표시 할 수있는 TensorBoard라는 유틸리티를 제공합니다. 다음은 TensorBoard가 그래프를 시각화하는 방법을 보여주는 스크린 샷입니다.
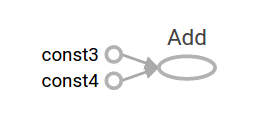
+텐서보드의 설치 및 활용 법은 추후 게시글에 올리도록 하겠습니다. 데이터의 흐름도의 이해를 위해 스크린샷 처럼 표시되는구나 정도로 일단 이해하시고 넘어가시면 됩니다.
이 도표는 항상 일정한 결과를 산출하기 때문에 특히 흥미 롭지 않습니다. 자리 표시 자라고하는 외부 입력을 허용하도록 그래프를 매개 변수화 할 수 있습니다. 자리 표시자는 나중에 값을 제공하겠다는 약속입니다.
a = tf.placeholder(tf.float32)
b = tf.placeholder(tf.float32)
adder_node = a + b # + provides a shortcut for tf.add(a, b)
앞의 세 줄은 함수 또는 람다와 비슷하지만 두 개의 입력 매개 변수 (a 및 b)를 정의한 다음 해당 매개 변수에 대한 연산을 정의합니다. feed_dict 매개 변수를 사용하여 이러한 입력란에 구체적인 값을 제공하는 Tensors를 지정하여이 그래프를 여러 입력으로 평가할 수 있습니다.
print(sess.run(adder_node, {a: 3, b:4.5}))
print(sess.run(adder_node, {a: [1,3], b: [2, 4]}))

+ 출력 결과 물은 봣을 때 첫 번쨰 명령 문의 계산식은
3+ 4.5 이고
두번째 계산은
a: 1 + b: 2 = 3
a: 3 + b: 4 = 7
의 결과값을 표현하는 것입니다.
In TensorBoard, the graph looks like this:
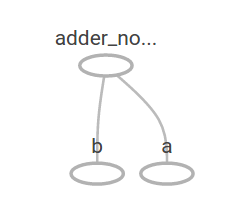
다른 연산을 추가하여 계산 그래프를 더 복잡하게 만들 수 있습니다. 예를 들어,
add_and_triple = adder_node * 3.
print(sess.run(add_and_triple, {a: 3, b:4.5}))
add_and_triple = adder_node * 3.
print(sess.run(add_and_triple, {a: 3, b:4.5}))
add_and_triple = adder_node * 3.
print(sess.run(add_and_triple, {a: 3, b:4.5}))

+ 연산 : (3+4.5)*3
The preceding computational graph would look as follows in TensorBoard:
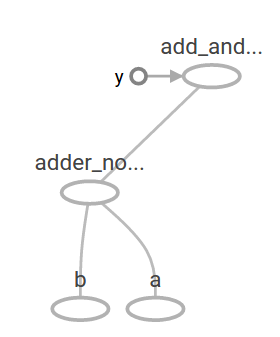
기계 학습에서 우리는 전형적으로 위와 같은 임의의 입력을 취할 수있는 모델을 원할 것입니다. 모델을 학습 가능하게 만들려면 동일한 입력으로 새로운 출력을 얻기 위해 그래프를 수정할 수 있어야합니다. 변수를 사용하면 그래프에 학습 가능한 매개 변수를 추가 할 수 있습니다. 그것들은 타입과 초기 값으로 구성됩니다 :
W = tf.Variable([.3], tf.float32)
b = tf.Variable([-.3], tf.float32)
x = tf.placeholder(tf.float32)
linear_model = W * x + b
상원 의원은 제소자를 호출 할 때 값이 변하지 않을 것입니다. 반대로 할 수 없습니다. TensorFlow 프로그램의 모든 변수를 다음과 같이 사용하십시오.
init = tf.global_variables_initializer()
sess.run(init)
init이 모든 전역 변수를 초기화하는 TensorFlow 하위 그래프의 핸들임을 인식하는 것이 중요합니다. sess.run을 호출 할 때까지 변수는 초기화되지 않습니다.
x는 자리 표시 자이므로 다음과 같이 x의 여러 값에 대해 linear_model을 동시에 평가할 수 있습니다.
print(sess.run(linear_model, {x:[1,2,3,4]}))

+ x를 순차적으로 대입하면서 출력하는 것을 볼 수 있습니다.
우리는 모델을 만들었지 만 아직 얼마나 좋은지 모릅니다. 훈련 데이터에 대한 모델을 평가하려면 원하는 값을 제공하기 위해 y 자리 표시자가 필요하며 손실 함수를 작성해야합니다.
손실 함수는 제공된 모델로부터 현재 모델이 얼마나 떨어져 있는지를 측정합니다. 현재 모델과 제공된 데이터 사이의 델타의 제곱을 합한 선형 회귀에 표준 손실 모델을 사용합니다. linear_model - y는 각 요소가 해당 예제의 오류 델타 인 벡터를 만듭니다. tf.square를 호출하여 오류를 제곱합니다. 그런 다음 모든 제곱 된 오류를 합하여 tf.reduce_sum을 사용하여 모든 예제의 오류를 추상화하는 단일 스칼라를 만듭니다.
y = tf.placeholder(tf.float32)
squared_deltas = tf.square(linear_model - y)
loss = tf.reduce_sum(squared_deltas)
print(sess.run(loss, {x:[1,2,3,4], y:[0,-1,-2,-3]}))

W와 b의 값을 -1과 1의 완벽한 값으로 재 할당하여 수동으로 향상시킬 수 있습니다. 변수는 tf.Variable에 제공된 값으로 초기화되지만 tf.assign과 같은 연산을 사용하여 변경할 수 있습니다. 예를 들어, W = -1 및 b = 1은 우리 모델에 대한 최적의 매개 변수입니다. 그에 따라 W와 B를 변경할 수 있습니다.
fixW = tf.assign(W, [-1.])
fixb = tf.assign(b, [1.])
sess.run([fixW, fixb])
print(sess.run(loss, {x:[1,2,3,4], y:[0,-1,-2,-3]}))

마지막 인쇄는 손실이 0임을 보여줍니다.
우리는 W와 B의 "완벽한"값을 추측했지만 기계 학습의 요점은 올바른 모델 매개 변수를 자동으로 찾는 것입니다. 다음 섹션에서이를 수행하는 방법을 보여줄 것입니다.
+ 지금은 손실이 0 인 것인 것처럼 간단한 계산식으로 했지만, 나중에 갈 수록 소수도 나오고 손실율도 커서 더 정확한 모듈을 만들기 위한 작업을 하겠습니다.
+ 일단 이번 글에서는 간단한 이해 및 원리만 이해하시면 되겠습니다.






















